The perimeter of snowflake island is infinite
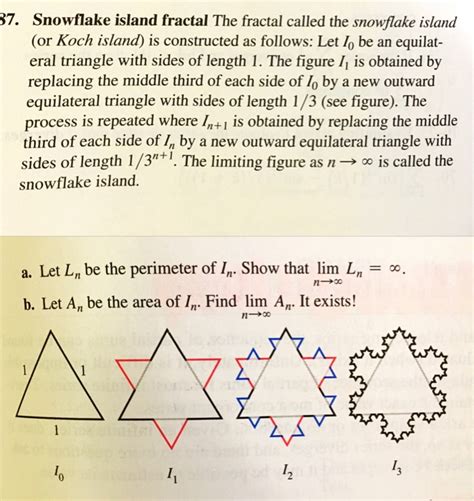
Perimeter of the Koch snowflake Each iteration multiplies the number of sides in the Koch snowflake by four, so the number of sides after $${\displaystyle n}$$ iterations is given by: If the original equilateral triangle has sides of length $${\displaystyle s}$$, the length of each side of the snowflake after $${\displaystyle … Visa mer The Koch snowflake (also known as the Koch curve, Koch star, or Koch island ) is a fractal curve and one of the earliest fractals to have been described. It is based on the Koch curve, which appeared in a 1904 paper titled "On a … Visa mer The Koch snowflake can be constructed by starting with an equilateral triangle, then recursively altering each line segment as follows: 1. divide … Visa mer A turtle graphic is the curve that is generated if an automaton is programmed with a sequence. If the Thue–Morse sequence members are used in order to select program states: • If $${\displaystyle t(n)=0}$$, move ahead by one unit, Visa mer Following von Koch's concept, several variants of the Koch curve were designed, considering right angles (quadratic), other angles (Cesàro), circles and polyhedra and their extensions to higher dimensions (Sphereflake and Kochcube, respectively) Squares can be used … Visa mer It is possible to tessellate the plane by copies of Koch snowflakes in two different sizes. However, such a tessellation is not possible using only … Visa mer The Koch curve can be expressed by the following rewrite system (Lindenmayer system): Alphabet : F Constants : +, − Axiom : F Production rules: F → F+F--F+F Here, F means "draw forward", - means "turn right 60°", and + … Visa mer • List of fractals by Hausdorff dimension • Gabriel's Horn (infinite surface area but encloses a finite volume) Visa mer WebbHowever, at every stage in building the snowflake, the perimeter is multiplied by 4/3 - it is always increasing. So the ideal snowflake (ideal meaning you go through an infinite number of stages constructing the figure) has an infinite perimeter (initial perimeter * 4/3 * 4/3 * 4/3 * ...) yet a finite area. Its not a paradox; its simply a fractal.
The perimeter of snowflake island is infinite
Did you know?
Webb16 mars 2024 · Notes: I have very extensive notes at the end of the Fanfiction site's version of this story. The reason they're not posted here is that the notes exceed the 5000 character limit on end notes for a chapter. Webb2 apr. 2024 · Kunlun Mountain and Jinao Island are two giants, like two huge space battleships , navigating through the air.And keep getting closer.99.72 of the turrets can still be used, the protective cover can be used continuously for about 108 hours, and 100 flying magic weapons are on standby Everything is ready, everything is as I expected A …
WebbQuiz #10 (Form A) KEY ANSWERS ARE IN BOLD ITALICS. 1) Which number is next in the Fibonacci sequence of numbers: 1, 1, 2, 3, 5, 8, 13, 21 . . a) 55 b) 34 c) 8 d) 1.62 2) Which … Webb2 apr. 2024 · Infinite Perimeter, an as-yet-unfinished series which looks at a decade of ... This idea is thrown into stark relief by the refugee crisis so familiar to residents of the …
WebbVIDEO ANSWER:hizo today and this question we're looking at something that could be called Snowflake Island. So what it is is a equilateral triangle that has, of course, the re … WebbInfinite Border, Finite Area Koch's snowflake is a quintessential example of a fractal curve, a curve of infinite length in a bounded region of the plane. Not every bounded piece of …
WebbThe Koch Snowflake has an infinite perimeter, but all its squiggles stay crumpled up in a finite area. So how big is this finite area, exactly? To answer that, let’s look again at The …
WebbThe total area of the snowflake uses the infinite sequence . We will add all the terms of the series together, and add 1, to produce the following sum Seeing that this is a geometric … cannot convert from iconfiguration to actionWebbThe Koch snowflake is contained in a bounded region — you can draw a large circle around it — so its interior clearly has finite area. As for the perimeter, it isn't quite right to say the boundary has "infinite perimeter". The Koch snowflake is constructed iteratively, and at each step, the perimeter of that iteration is 4/3 times the ... fj cruiser mechanic scottsdaleWebb• Area and perimeter • Spatial relationships and geometric shapes • Data ... snowflakes, and even the distinct breeds of dogs reveal God’s principle of individuality. Each child’s uniqueness is manifest through his external ... Vol. I and II, Literacy Unlimited. (ISBN: 0-9643210-3-3 and 1-885942-31-1) Publishable or ... cannot convert from initializer list to intWebbKeep reading to understand more about Area of infinite koch snowflake and how to use it. order now. ... The Koch Snowflake has an infinite perimeter, but all its squiggles stay crumpled up in a finite area. ... Koch star, or Koch island) is a fractal curve and one of the earliest fractals to have been described. cannot convert from initializer list toWebbRecall that. The snowflake island is a region enclosed with a snowflake curve.. Since the island is bounded by the curve - contained in an enclosed region - its interior has a finite … cannot convert from int to boolean翻译WebbAmazing properties of fractals: Koch Snowflake perimeter - YouTube 0:00 / 6:22 Amazing properties of fractals: Koch Snowflake perimeter fractalmath 2.62K subscribers Subscribe 63K views 12... fj cruiser mirror light bulb sizeWebb24 mars 2024 · The Koch snowflake is a fractal curve, also known as the Koch island, which was first described by Helge von Koch in 1904. It is built by starting with an … cannot convert from string to boolean talend